ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ

СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ

Рассмотрим работу программы на примере исследования СМО, моделирующей работу морского порта. Данная модель находится в файле «model1.qsf» в архиве примеров.

1. Задание на моделирование.

Рассмотрим морской порт, в который на разгрузку приходят корабли. Время прихода кораблей в порт распределено нормально с математическим ожиданием m = 1 и средним квадратическим отклонением σ = 0,3. Разгрузка каждого судна осуществляется около одного из 7 причалов, каждый из которых может обслуживать одновременно только одно судно. Судно, приходящее в порт, становится под разгрузку к освободившемуся причалу, а если все причалы заняты, то оно становится в очередь на рейде. Количество судов на рейде не должно превышать 10. Время разгрузки распределено равномерно. Каждый корабль относится к одной из 3 категорий: первой, второй или третьей. Преимущество разгрузки имеют суда с более высокой категорией. Данные о кораблях всех категорий приведены в таблице 1.

Таблица 1 – Данные о категориях кораблей

Категория судна	Вероятность появления	Минимальная продолжительность разгрузки, ч	Максимальная продолжительность разгрузки, ч
I	0.1	4	6
II	0.4	6	8
III	0.5	8	10

Необходимо провести моделирование работы порта для оценки эффективности его функционирования и определения оптимального числа причалов.

2. Проектирование структуры СМО.

Представим порт в виде имитационной модели СМО в среде моделирования. Каждому объекту предметной области поставим в соответствие объект модели, как показано в таблице 2.

Таблица 2 – Соответствие объектов предметной области и объектов модели

Объект предметной области	Объект модели
Поток приходящих кораблей	Генератор «Поток кораблей»
Очередь кораблей на рейде	Накопитель «Рейд»
Причалы	Канал «Причалы»
Поток разгруженных кораблей	Сток «Сток обслуживания»
Поток кораблей, получивших отказ в ожидании на рейде	Сток «Сток отказов»
Корабли I категории	Тип заявки «Корабли 1 категории»
Корабли II категории	Тип заявки «Корабли 2 категории»
Корабли III категории	Тип заявки «Корабли 3 категории»

Таким образом, структура модели в среде моделирования будет иметь вид, представленный на рисунке 1.

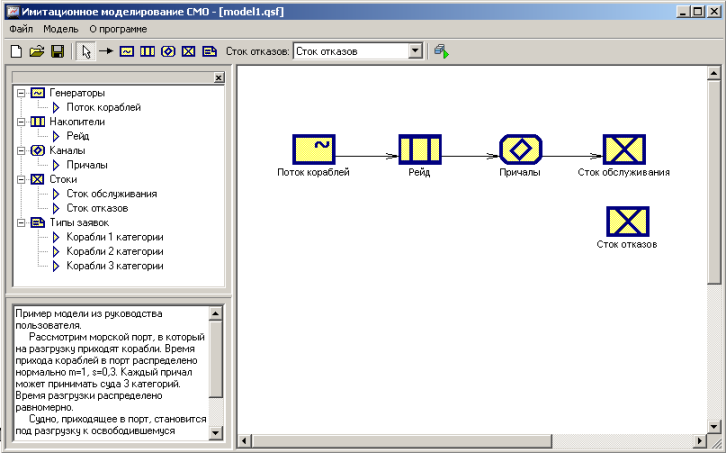
Из генератора, моделирующего приход кораблей, заявки поступают в накопитель. Если накопитель уже содержит 10 заявок (очередь на рейде ограничена 10 кораблями), то поступающие заявки получают отказ в обслуживании и переходят в сток отказов. Иначе заявки либо ожидают обслуживания в накопителе, если в канале нет свободных обслуживающих устройств (т.е. если нет свободных причалов), либо сразу переходят на обслуживание в канал, если свободные обслуживающие устройства имеются. После обслуживания (разгрузки) заявки переходят в сток обслуживания, где ведется их подсчет.

3. Установка параметров модели.

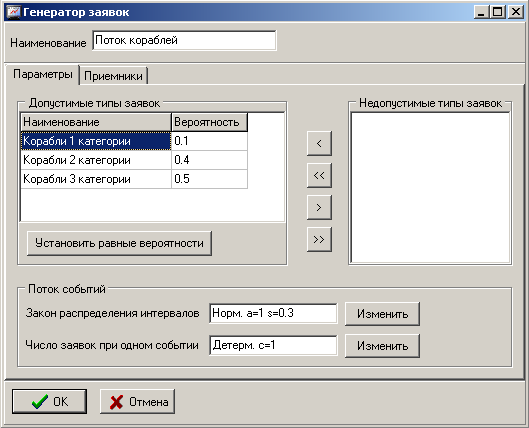
Для генератора установим закон распределения интервалов между моментами генерации заявок и вероятности появления каждого типа заявки, как изображено на рисунке 2. При каждом событии генерации появляется одна заявка. Дисциплина выбора приемника в данном случае не имеет значения, так как он всего один – накопитель «Рейд».

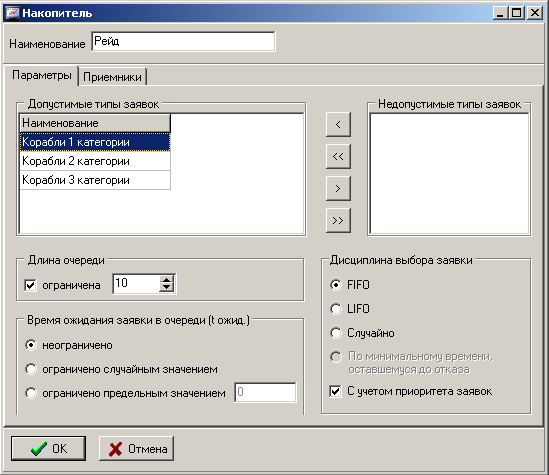
Для накопителя установим ограничение на длину очереди, дисциплину ожидания, дисциплину выбора заявки в соответствии с рисунком 3. Так как корабли в соответствии категорий имеют приоритет в обслуживании, то необходимо отметить признак учета приоритета заявок.

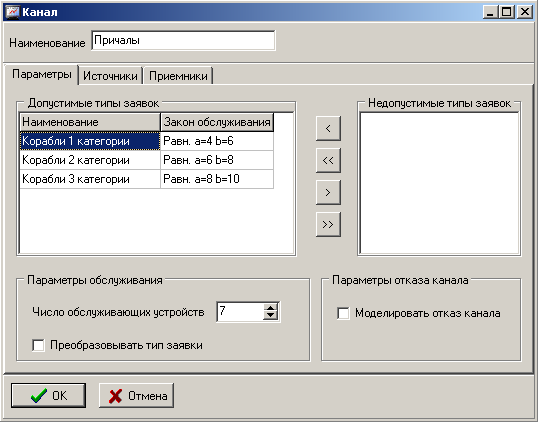
Для канала установим законы распределения времени обслуживания и число обслуживающих устройств, как показано на рисунке 4.

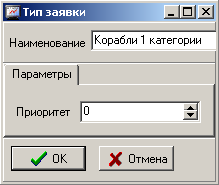
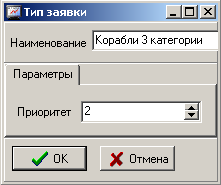
Для стоков нет необходимости устанавливать специфические параметры. Для типов заявок установим приоритеты, как показано на рисунке 5.

4. Выполнение эксперимента и анализ результатов.

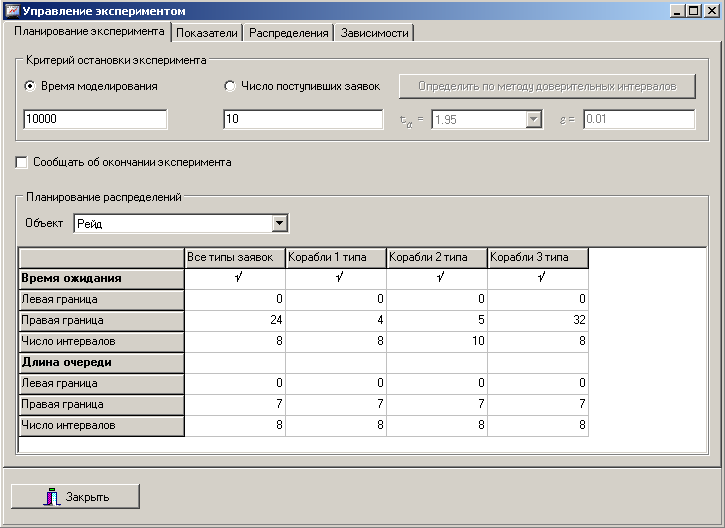
Следующим этапом исследования является настройка условий эксперимента. Так как никаких ограничений на объем выборки и время моделирования в задании не указано, установим критерий окончания моделирования по времени моделирования, которое для обеспечения высокой точности вычислений примем 10000 часов. Для оценки разброса значений времени ожидания кораблей на рейде, выберем соответствующее распределение, как показано на рисунке 6.

Произведем расчет показателей эффективности СМО. Для этого перейдем на вкладку «Показатели» и выполним имитационный эксперимент (прогон модели во времени). Результаты эксперимента сохраним в текстовый файл. Значения основных показателей представлены в таблице 3.

Таблица 3 – Основные результаты моделирования

Коэффициент загрузки канала	100%
Количество заявок, попавших в сток отказов (т.е. кораблей, получивших отказ в обслуживании)	10%
Среднее время ожидания в очереди на рейде	9,35 ч

Время ожидания кораблей на рейде и процент отказов имеют достаточно высокие значения. Поэтому можно сделать вывод, что СМО не справляется с потоком заявок или перегружена.

Для просмотра гистограмм выбранных распределений перейдем на вкладку «Распределения». Для одного из распределений (распределения времени ожидания кораблей I категории на рейде) проверим гипотезу о виде закона распределения.

Исходя из характера гистограммы разумно предположить, что для описания данного распределения подойдет показательный закон. Единственным параметром данного закона является интенсивность. Подобрать значение параметра вручную достаточно трудно, поэтому воспользуемся автоматическим расчетом. Для этого выберем показательный закон в выпадающем списке «Закон распределения» и нажмем кнопку «Вычислить параметры». Получим значение λ = 0,98.

Таким образом, мы предполагаем, что распределения времени ожидания кораблей I категории на рейде подчиняется показательному закону с λ = 0,98. Чтобы проверить это предположение, нужно нажать кнопку «Проверить гипотезу». В результате будет выдано сообщение, как показано на рисунке 7.

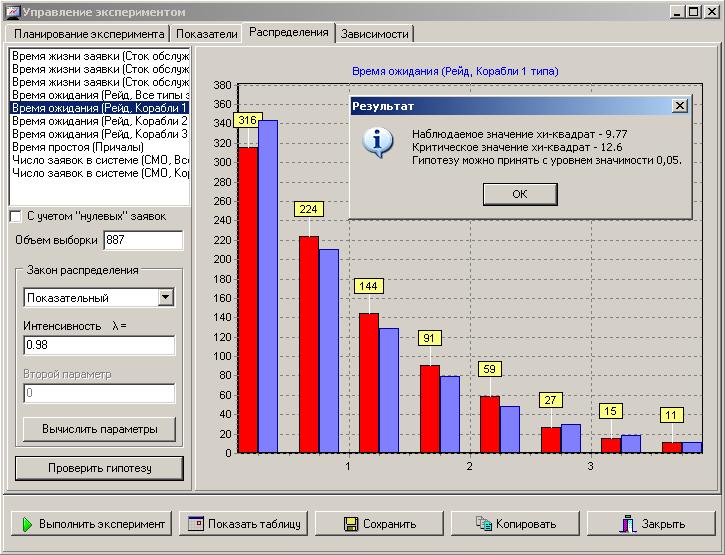
Очевидно, гипотеза была принята.

5. Поиск оптимальных значений параметров СМО.

В целях оптимизации работы СМО определим число причалов, необходимое для работы порта без перегрузки и простоя. Для этого найдем зависимости среднего времени ожидания кораблей на рейде и среднего времени простоя причалов от количества причалов в порту. С этой целью перейдем на вкладку «Зависимости». В качестве параметра определим число обслуживающих устройств, в качестве зависимых показателей - время ожидания заявок в накопителе и время простоя обслуживающих устройств в канале, как показано на рисунке 8.

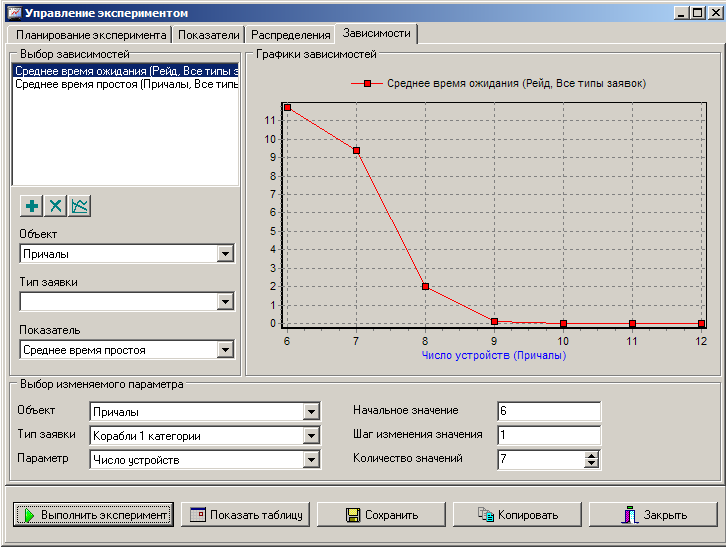
Для выполнения эксперимента нажмем кнопку «Выполнить экспермент» и рассмотрим построенные графики. График зависимости среднего времени ожидания заявок в накопителе от количества обслуживающих устройств в канале приведен на рисунке 8. График зависимости времени простоя обслуживающих устройств от количества обслуживающих устройств в канале представлен на рисунке 9 (данное изображение получено с помощью функции копирования графика, фон графика можно изменить, кликнув на нем правой кнопкой мыши).

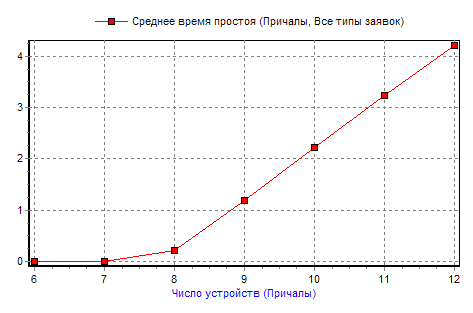
Так же представим построенные зависимости в виде сводной таблицы. Для этого нужно выделить в списке оба отклика и нажать кнопку «Показать таблицу», после чего в окне вывода таблиц нажать кнопку «Копировать». Результат копирования представлен в таблице 4.

Таблица 4 – Зависимости показателей СМО от числа обслуживающих устройств

Число устройств (Причалы)	6	7	8	9	10	11	12
Среднее время ожидания (Рейд, Все типы заявок)	11,7	9,37	2,08	0,141	0,0183	0,00202	0,000155
Среднее время простоя (Причалы, Все типы заявок)	0,00153	0,00232	0,199	1,18	2,18	3,2	4,23

Таким образом, проанализировав зависимости можно прийти к выводу, что для эффективного функционирования порта необходимо наличие 8 или 9 причалов. В первом случае более рационально используются ресурсы порта (причалы). Второй случай соответствует более высокому качеству обслуживания.

Вернуться на главную страницу